Пространственные системы координат (ОП СРНС, лекция)

Конечная функция СРНС - ответить на вопросы "где?" и "когда?" применительно к потребителю. Ответом может послужить и некоторое контекстное описание, но удобнее пользоваться абстракцией координат.

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

Существует значительное многообразие типов систем координат, отличающихся законом связи координат и положения в пространстве. В приложениях СРНС наиболее востребованы прямоугольные и эллипсоидальные системы координат.

Перед СРНС ставится задача определения трех пространственных координат и одной временной (времени). Начнем с изучения различных пространственных систем координат, используемых в СРНС.

Локальная декартова система координат

Декартова система координат - это прямоугольная система координат с равным масштабом по различным осям.

Для определения декартовой системы координат достаточно задать:

• положение начала системы координат $O$;
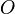• направление осей $OX$, $OY$, $OZ$;
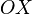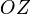• масштаб по осям.

Геоцентрическая неинерциальная система координат

Общепризнанное международное название систем координат данного типа - ECEF (Earth Centered, Earth Fixed). Как следует из названия, геоцентрическая неинерциальная система координат 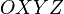$OXYZ$ жестко связана с Землей и имеет начало в её центре масс. В этой системе координат удобно описывать положение точек, находящихся на земле, или движущихся вблизи её.

Ось 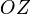$OZ$ направлена по оси вращения Земли в сторону Северного полюса.

Геоцентрическая инерциальная система координат

Для обеспечения работоспособности СРНС необходимо производить расчет и прогноз положения навигационных аппаратов. Их движение, в первом приближении, описывается уравнениями Ньютоновской механики, которые справедливы в инерциальной системе координат.

Любая система координат, которая жестко связана с Землей, существенно отлична от инерционной в масштабах движения космических аппаратов. Примерно за сутки эта система координат успевает развернуться относительно инерционных.