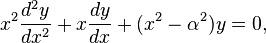Функции Бесселя — различия между версиями
Korogodin (обсуждение | вклад) (Новая страница: «'''Функции Бесселя''' в математике — семейство функций, являющихся каноническими решениям...») |
Korogodin (обсуждение | вклад) |
||
| Строка 59: | Строка 59: | ||
тогда с учетом того, что подынтегральная функция в полученном выражении для <math>\!\! J </math> периодична и её период совпадает с периодом интегрирования, а значит замена аргумента <math>\!\! \phi_k </math> на <math>\!\! \phi_k + \psi_k </math> не меняет значения интеграла, получаем выражение: | тогда с учетом того, что подынтегральная функция в полученном выражении для <math>\!\! J </math> периодична и её период совпадает с периодом интегрирования, а значит замена аргумента <math>\!\! \phi_k </math> на <math>\!\! \phi_k + \psi_k </math> не меняет значения интеграла, получаем выражение: | ||
<math>J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).</math> | <math>J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).</math> | ||
| + | |||
| + | [[Категория:Статистическая радиотехника]] | ||
Версия 22:40, 16 апреля 2011
Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
где  — произвольное вещественное число, называемое порядком.
— произвольное вещественное число, называемое порядком.
Модифицированные функции Бесселя
Модифици́рованные фу́нкции Бе́сселя — это функции Бесселя от чисто мнимого аргумента.
Первого рода:
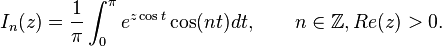
Модифицированные функции Бесселя первого рода при синтезе некогерентных систем
При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида:
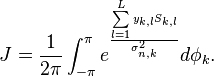
Рассмотрим подробнее числитель экспоненты для типичной модели сигнала
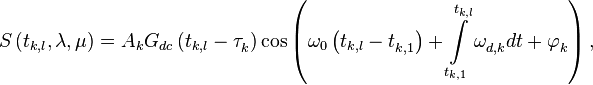
тогда
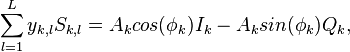
где
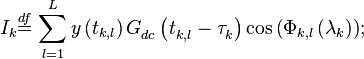
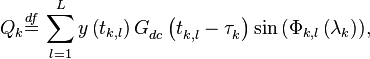
в которых
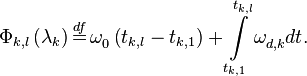
Далее производится красивый хак: очевидно, что 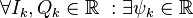 , такая что:
, такая что:
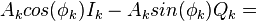
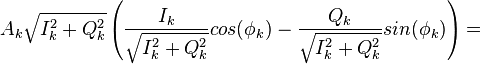
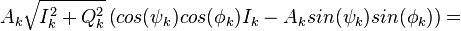
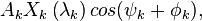
где
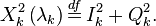
С учетом проделанных преобразованием, можно записать:
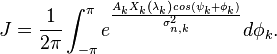
По определению, модифицированная функция Бесселя первого рода нулевого порядка:
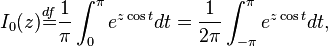
тогда с учетом того, что подынтегральная функция в полученном выражении для 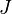 периодична и её период совпадает с периодом интегрирования, а значит замена аргумента
периодична и её период совпадает с периодом интегрирования, а значит замена аргумента 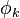 на
на 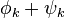 не меняет значения интеграла, получаем выражение:
не меняет значения интеграла, получаем выражение: