Дискриминатор задержки NELP — различия между версиями
Материал из SRNS
Dneprov (обсуждение | вклад) (→Листинг модели) |
Dneprov (обсуждение | вклад) (→Листинг модели) |
||
| Строка 41: | Строка 41: | ||
[[File:20140327 DZO q35,T=20ms,delta=chip5.png|center|600px]] | [[File:20140327 DZO q35,T=20ms,delta=chip5.png|center|600px]] | ||
| − | |||
| − | |||
{|table class="wikitable collapsible collapsed" | {|table class="wikitable collapsible collapsed" | ||
| − | ! colspan =" | + | ! colspan ="1"| Листинг модели |
| + | <source lang = matlab> | ||
| + | close all; | ||
| + | clear | ||
| + | clc | ||
| + | |||
| + | global tauChip | ||
| + | tauChip = 1e-3/511; % Длительность чипа | ||
| + | |||
| + | NoiseEnable = 1; | ||
| + | |||
| + | Np = 1000; | ||
| + | |||
| + | Tc = 0.001; % Период интегрирования в корреляторе | ||
| + | |||
| + | qcno_dB = 45; | ||
| + | stdn_IQ = 1; % СКО шума квадратурных сумм | ||
| + | |||
| + | qcno = 10^(qcno_dB/10); | ||
| + | A_IQ = stdn_IQ * sqrt(2 * qcno * Tc); | ||
| + | |||
| + | tauIst = tauChip/5; | ||
| + | deltaTau = tauChip/10; | ||
| + | |||
| + | Dp=stdn_IQ^2; % Дисперсия promt компоненты | ||
| + | Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late | ||
| + | Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late | ||
| + | |||
| + | L=chol([Dp Dpe Dpe; % �спользуем разложение Холецкого | ||
| + | Dpe Dp Del; | ||
| + | Dpe Del Dp])'; | ||
| + | |||
| + | |||
| + | tauExtr= [tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip]; | ||
| + | NtauExtr = length(tauExtr); | ||
| + | |||
| + | EpsPhi = 1*rand(1,1)*2*pi; | ||
| + | EpsW = 1*10*2*pi; | ||
| + | |||
| + | SdTeor = 2*qcno*Tc*sinc(EpsW*Tc/2 /pi)^2*[4/tauChip - 2*(deltaTau/tauChip^2)]; % Теоретическая крутизна | ||
| + | |||
| + | Ud = zeros(1,NtauExtr); | ||
| + | Udteor = zeros(1,NtauExtr); | ||
| + | |||
| + | p = nan(1,NtauExtr); | ||
| + | p_early = nan(1,NtauExtr); | ||
| + | p_late = nan(1,NtauExtr); | ||
| + | EpsTau = nan(1,NtauExtr); | ||
| + | |||
| + | for k = 1:NtauExtr | ||
| + | |||
| + | EpsTau(k) = tauIst - tauExtr(k); | ||
| + | |||
| + | p(k) = ro(EpsTau(k)); | ||
| + | p_late(k) = ro(EpsTau(k)+deltaTau/2); | ||
| + | p_early(k) = ro(EpsTau(k)-deltaTau/2); | ||
| + | |||
| + | for n = 1:Np | ||
| + | |||
| + | nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы | ||
| + | nQ = L* randn(3,1); | ||
| + | |||
| + | mI = A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIe = A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | mIl = A_IQ*p_late(k) *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | mQ = -A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQe = -A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | mQl = -A_IQ*p_late(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); | ||
| + | |||
| + | I = mI + NoiseEnable*nI(1,1); | ||
| + | Ie = mIe + NoiseEnable*nI(2,1); | ||
| + | Il = mIl + NoiseEnable*nI(3,1); | ||
| + | Q = mQ + NoiseEnable*nQ(1,1); | ||
| + | Qe = mQe + NoiseEnable*nQ(2,1); | ||
| + | Ql = mQl + NoiseEnable*nQ(3,1); | ||
| + | |||
| + | Ud(k) = Ud(k) + (Ie^2-Il^2) + (Qe^2-Ql^2); | ||
| + | end | ||
| + | Udteor(k) = 2*qcno*Tc*(sinc(EpsW*Tc/2 /pi)^2)*(p_early(k)^2 - p_late(k)^2); | ||
| + | if ~mod(k,100) | ||
| + | fprintf('Progress: %.2f %%\n', k*100/NtauExtr) | ||
| + | end | ||
| + | end | ||
| + | |||
| + | plot(EpsTau/tauChip, [Ud/Np; Udteor; SdTeor*EpsTau]) | ||
| + | xlabel('\epsilon_{tau}/\tau_{chip}') | ||
| + | ylim([min(Udteor)-10 max(Udteor)+10]) | ||
| + | grid on | ||
| + | |||
| + | </source> | ||
|} | |} | ||
Версия 21:22, 27 марта 2014
Описание дискриминатора
Non-coherent Early minus Late Power (NELP) - некогерентный дискриминатор задержки, описываемый следующим соотношением:
 ,
,
где
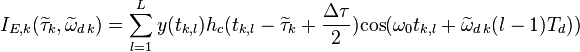 ,
,
 ,
,
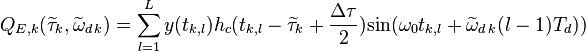 ,
,
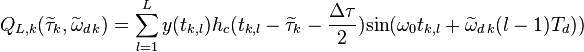 .
.
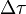 - сдвиг дальномерного кода между запаздывающей и опережающей компонентами.
- сдвиг дальномерного кода между запаздывающей и опережающей компонентами.
Дискриминационная характеристика
Дискриминационная характеристика описывается выражением
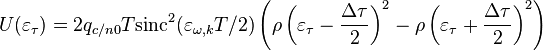 .
.
Ее крутизна 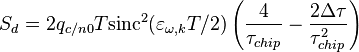 .
.
Для проверки формул составлена модель в Matlab.
В модели принято:
- длительность символа дальномерного кода
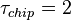 мкс,
мкс,
- расстройка по частоте
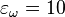 Гц,
Гц,
- каждая точка моделируемой дискриминационной характеристики усреднялась 1000 раз.
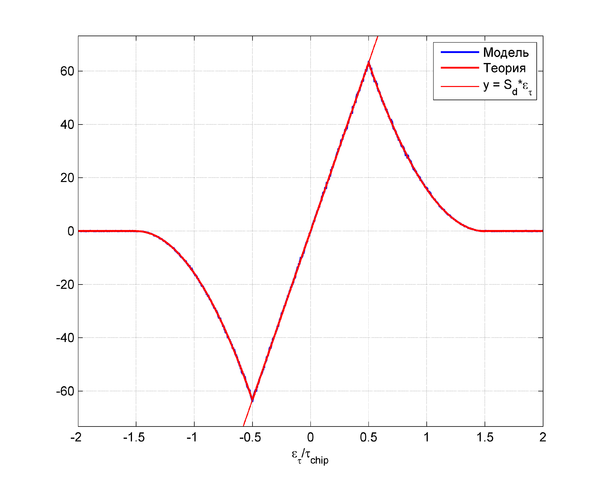
Результат моделирования для 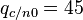 дБГц,
дБГц, 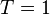 мс,
мс, 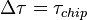 :
:
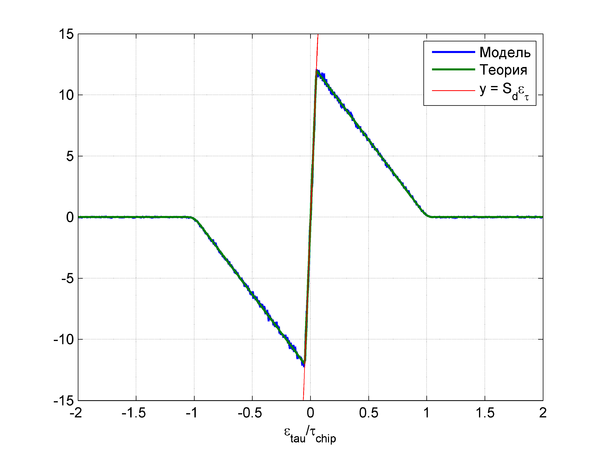
Результаты моделирования для 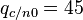 дБГц,
дБГц, 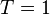 мс,
мс, 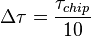 :
:
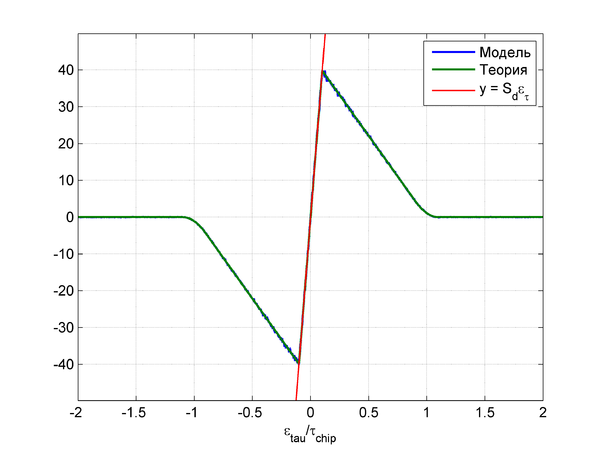
Результаты моделирования для  дБГц,
дБГц, 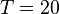 мс,
мс, 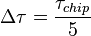 :
:
| Листинг модели
close all; clear clc global tauChip tauChip = 1e-3/511; % Длительность чипа NoiseEnable = 1; Np = 1000; Tc = 0.001; % Период интегрирования в корреляторе qcno_dB = 45; stdn_IQ = 1; % СКО шума квадратурных сумм qcno = 10^(qcno_dB/10); A_IQ = stdn_IQ * sqrt(2 * qcno * Tc); tauIst = tauChip/5; deltaTau = tauChip/10; Dp=stdn_IQ^2; % Дисперсия promt компоненты Dpe=ro(deltaTau/2)*stdn_IQ^2; % Взаимная дисперсия promt-early/late Del=ro(deltaTau)*stdn_IQ^2; % Взаимная дисперсия early-late L=chol([Dp Dpe Dpe; % �спользуем разложение Холецкого Dpe Dp Del; Dpe Del Dp])'; tauExtr= [tauIst-2*tauChip:4*tauChip/1000:tauIst+2*tauChip]; NtauExtr = length(tauExtr); EpsPhi = 1*rand(1,1)*2*pi; EpsW = 1*10*2*pi; SdTeor = 2*qcno*Tc*sinc(EpsW*Tc/2 /pi)^2*[4/tauChip - 2*(deltaTau/tauChip^2)]; % Теоретическая крутизна Ud = zeros(1,NtauExtr); Udteor = zeros(1,NtauExtr); p = nan(1,NtauExtr); p_early = nan(1,NtauExtr); p_late = nan(1,NtauExtr); EpsTau = nan(1,NtauExtr); for k = 1:NtauExtr EpsTau(k) = tauIst - tauExtr(k); p(k) = ro(EpsTau(k)); p_late(k) = ro(EpsTau(k)+deltaTau/2); p_early(k) = ro(EpsTau(k)-deltaTau/2); for n = 1:Np nI = L * randn(3,1); % Применяем результат разложения Холецкого и получаем коррелированные шумы nQ = L* randn(3,1); mI = A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); mIe = A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); mIl = A_IQ*p_late(k) *sinc(EpsW*Tc/2 /pi) * cos(EpsW*Tc/2 + EpsPhi); mQ = -A_IQ * p(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); mQe = -A_IQ*p_early(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); mQl = -A_IQ*p_late(k) * sinc(EpsW*Tc/2 /pi) * sin(EpsW*Tc/2 + EpsPhi); I = mI + NoiseEnable*nI(1,1); Ie = mIe + NoiseEnable*nI(2,1); Il = mIl + NoiseEnable*nI(3,1); Q = mQ + NoiseEnable*nQ(1,1); Qe = mQe + NoiseEnable*nQ(2,1); Ql = mQl + NoiseEnable*nQ(3,1); Ud(k) = Ud(k) + (Ie^2-Il^2) + (Qe^2-Ql^2); end Udteor(k) = 2*qcno*Tc*(sinc(EpsW*Tc/2 /pi)^2)*(p_early(k)^2 - p_late(k)^2); if ~mod(k,100) fprintf('Progress: %.2f %%\n', k*100/NtauExtr) end end plot(EpsTau/tauChip, [Ud/Np; Udteor; SdTeor*EpsTau]) xlabel('\epsilon_{tau}/\tau_{chip}') ylim([min(Udteor)-10 max(Udteor)+10]) grid on |
|---|