Пространственные системы координат (ОП СРНС, лекция) — различия между версиями

Версия 00:26, 13 сентября 2013

Конечная функция СРНС - ответить на вопросы "где?" и "когда?" применительно к потребителю. Ответом может послужить и некоторое контекстное описание, но удобнее пользоваться абстракцией координат.

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

Существует значительное многообразие типов систем координат, отличающихся законом связи координат и положения в пространстве. В приложениях СРНС наиболее востребованы прямоугольные и эллипсоидальные системы координат.

Перед СРНС ставится задача определения трех пространственных координат и одной временной (времени). Начнем с изучения различных пространственных систем координат, используемых в СРНС.

Виды пространственных систем координат

Локальная декартова система координат

Декартова система координат - это прямоугольная система координат с равным масштабом по различным осям.

Для определения декартовой системы координат достаточно задать:

• положение начала системы координат ;
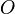• направление осей , , ;
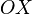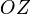• масштаб по осям.

Декартова система координат, связанная с объектом

Геоцентрическая неинерциальная прямоугольная система координат

Общепризнанное международное название систем координат данного типа - ECEF (Earth Centered, Earth Fixed). Как следует из названия, геоцентрическая неинерциальная система координат 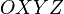жестко связана с Землей и имеет начало в её центре масс.

Ось 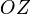направлена по оси вращения Земли в сторону Северного полюса.

Ось 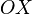лежит в плоскости земного экватора, связана с нулевым меридианом.

Ось дополняет систему координат до правой.

В этой системе координат удобно описывать положение точек, находящихся на земле или движущихся вблизи неё.

ECEF жестко связана с Землей и вращается с ней относительно инерциального пространства.

Существует множество разновидностей ECEF СК, отличающиеся принятым центром масс Земли, нулевым меридианом (об этом далее в разделе про геодезические СК).

Геодезическая система координат

Несмотря на то, что окружающее человека пространство трехмерно, нам удобнее пользоваться двухмерными картами. На то есть ряд причин:

• с двухмерными образами намного удобнее обращаться - создавать, использовать, хранить;
• человек использует не весь объем планеты, а лишь очень тонкую прослойку у поверхности.

Поверхность же эта, в первом приближении, очень близка к сфере. Рисунок дорог, домов, гор, рек и континентов с этой поверхности скопирован на карты.

Находить точку на карте удобнее по абсциссе и ординате на этой карте, а не координатам ECEF. Например, что можно сказать, без дополнительных расчетов, о местоположении точки (4366997, -4867716, 79259)? Или (2701898, -3375560, 4906826)? Где они на карте? На какой высоте расположены? В каком полушарии? Часовом поясе?

Система координат карт - геодезическая. Две координаты задают положение на эллипсоиде, аппроксимирующем земную поверхность, и одна координата - отклонение по высоте от этого эллипсоида (ENU - east, north, up). Но это качественно, а как перейти к конкретным числам?

Начало СК

Первым делом, необходимо определиться с началом системы координат - центром масс Земли.

Центр масс - центр инерции - геометрическая точка, положение которой характеризует распределение масс в теле или механической системе.

Центр масс Земли, или геоцентр, выбирается в качестве начала во многих системах координат, поскольку является очень устойчивой точкой в теле Земли. Эта точка реализуется по наблюдению спутников, движущихся в гравитационном поле Земли.

Геоцентр рекомендован в качестве начала для земной референцной системы в (IERS, 1996) и (IERS, 2003) как центр масс Земли, включая океаны и атмосферу.

Анализ спутниковых лазерных дальномерных наблюдений уверенно показывает, что система отсчета, реализованная в координатах станций наблюдений, неподвижных относительно земной коры, ощутимо смещается относительно центра масс Земли.

В 1997 г. МСВЗ провела кампанию по исследованию стабильности геоцентра, в которой приняли участие 42 исследователя из 25 научных групп, использовавших современные геофизические модели и результаты обработки лазерных измерений, GPS и DORIS.

По оценкам Ю.В. Баркина (ГАИШ), величина скоростей вековых движений в компонентах координат геоцентра составляет (IERS, 1999) около 1 см в столетие.

Вековые смещения в положении геоцентра можно объяснить такими причинами:

• изменением уровня моря;
• изменениями в ледяном щите (в Гренландии, Антарктиде);
• тектоническими смещениями в земной коре (постледниковая отдача, движение тектонических плит, субдукции и др.).

По результатам обработки реальных наблюдений выявлены годовые колебания в положении геоцентра (амплитуда около 4 мм по координатам X, Y и порядка 10 мм по Z), полугодовые, с периодами около 140, 60-70, 20 и 14 суток с амплитудами несколько миллиметров и с погрешностями амплитуд почти такого же порядка.

Движение отсчетной основы наземной сети относительно геоцентра поддается выявлению, но величина его небольшая, вероятно, не более 1 см по каждому из компонент. Учитывать изменения положения геоцентра в результатах измерений пока не рекомендовано (IERS, 1999).

Референц-эллипсоид

Предположим, что мы выбрали некоторый эллипсоид как аппроксимацию земного геоида. К слову, в России и

Датум

Набор параметров, связывающий ECEF и ENU, называется датумом или часто просто геодезической системой.

При работе с СРНС наиболее часто встречаются:

• WGS-84
• ПЗ.90.02
• СК-42
• ETRF-00

Геоцентрическая инерциальная система координат

Для обеспечения работоспособности СРНС необходимо производить расчет и прогноз положения навигационных аппаратов. Их движение, в первом приближении, описывается уравнениями Ньютоновской механики, которые справедливы в инерциальной системе координат.

Любая система координат, которая жестко связана с Землей, существенно отлична от инерционной в масштабах движения космических аппаратов. Примерно за сутки эта система координат успевает развернуться относительно инерционных.

Преобразование координат

Преобразование координат прямоугольных систем

Преобразование координат прямоугольных систем в геоцентрические

Ссылки

• Т.В. Бордовицына ТЕХНОЛОГИИ ГЛОБАЛЬНОГО ПОЗИЦИОНИРОВАНИЯ (GPS/ГЛОНАСС)
• Wiki. Geodetic system
• Wiki. ECEF
• Хабрахабр. Занимательная геодезия