Псевдодальномерный метод позиционирования (АП СРНС, лабораторная работа) — различия между версиями
Korogodin (обсуждение | вклад) (Новая страница: «== Цели работы == * Убедиться в работоспособности дальномерного и псевдодальномерного мет...») |
Korogodin (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
* Освоить методику расчета геометрического фактора снижения точности | * Освоить методику расчета геометрического фактора снижения точности | ||
| − | == | + | == Описание == |
| + | |||
| + | Назначение навигационной системы - определение координат, скорости, ориентации объекта-носителя, а так же обеспечение его шкалой времени. Для решения задачи оценки координат навигационного приемника, а так же коррекции его шкалы времени относительно системной, используется ''псевдодальномерный метод'' позиционирования. | ||
| + | |||
| + | === Дальномерный метод позиционирования === | ||
| + | |||
| + | Псевдодальномерный метод позиционирования спутниковых радионавигационных систем второго поколения является усложнением дальномерного метода позиционирования. Дальномерный метод позиционирования - это метод определения положения по измерениям дальности (расстояния) до нескольких точек с известными координатами. | ||
| + | |||
| + | {{pic|20121122_mayak1.png|Рисунок 1 - Карта, с нанесенной береговой линией и расположением маяков|pic1}} | ||
| + | |||
| + | |||
| + | Поясним суть дальномерного метода на примере. Представим, что потребитель - это корабль в море, которому для продолжения плавания требуется узнать где же он расположен. На корабле есть часы, по которым матросы узнают время. На берегу изобретательные люди установили два маяка, как показано на [[#pic1|рисунке 1]]). | ||
| + | |||
| + | Капитан предварительно договорился со смотрителем первого маяка, что ровно в полночь, и не наносекундой позже, тот подаст сигнал. Около полуночи матросы собрались вокруг корабельных часов, и как только получили сигнал - записали показания часов. На часах, естественно, было немного за полночь. Скажем, на <math>\Delta t_1</math>. Если известна скорость распространения сигнала <math>V</math>, то сразу можно сказать, что расстояние между первым маяком и кораблем составляет <math>R_1 = V \Delta t_1</math>. Тогда штурман может взять карту, циркуль и начертить окружность радиусом <math>R_1</math> вокруг первого маяка. | ||
| + | |||
| + | {{pic|20121122_mayak2.png|Рисунок 2 - Линия возможных положений после первого измерения|pic2}} | ||
| + | |||
| + | Уравнение этой окружности можно записать как: | ||
| + | ::<math>R_1 = \sqrt{(x - x_1)^2 + (y - y_1)^2}</math>,{{eqno|1}} | ||
| + | |||
| + | где <math>(x_1, y_1)</math> - координаты первого маяка. | ||
| + | |||
| + | В любой из точек окружности, что попали в море, может находиться корабль. Это уже лучше, чем полная неопределенность, но хотелось бы ограничиться одной возможной точкой. Для этого необходимо повторить измерения расстояния до второго маяка - получить оценку <math>R_2 = V \Delta t_2</math>. Множество возможных положений, при которых расстояние до второго маяка составляет <math>R_2</math> - ещё одна окружность. Её уравнение дополняет первое: | ||
| + | ::<math>R_2 = \sqrt{(x - x_2)^2 + (y - y_2)^2}</math>, {{eqno|2}} | ||
| + | |||
| + | где <math>(x_2, y_2)</math> - координаты второго маяка. | ||
| + | |||
| + | {{pic|20121122_mayak3.png|Рисунок 3 - Линия возможных положений после проведения двух измерения|pic3}} | ||
| + | |||
| + | Наш корабль должен одновременно находиться и на одной, и на другой окружности. Таких точек, а это точки пересечения окружностей, всего две. Но одна из них находится на суше, а морякам достаточно выглянуть за борт, чтобы понять, что они всё же в море. Остается один претендент - точка в море, которая и есть измеренное положение корабля. | ||
| + | |||
| + | <div style="background:#ffffff; border:1px dotted #8bcbff; padding:10px; margin-top:10px"> | ||
| + | '''Задача'''<br> | ||
| + | Предположим, что в качестве сигнала использовалась вспышка света, а расстояние до первого маяка составляет 1000 км. Что показали часы в первый раз? | ||
| + | </div> | ||
| + | |||
| + | <div style="background:#ffffff; border:1px dotted #8bcbff; padding:10px; margin-top:10px"> | ||
| + | '''Задача'''<br> | ||
| + | Допустим, часы на корабле запаздывают на 1 мс. Оцените вызванную этим фактом погрешность определения координат. | ||
| + | </div> | ||
Версия 14:48, 25 ноября 2012
Цели работы
- Убедиться в работоспособности дальномерного и псевдодальномерного методов позиционирования
- Реализовать одношаговый алгоритм решения навигационной задачи, убедиться в его работоспособности
- Освоить методику расчета геометрического фактора снижения точности
Описание
Назначение навигационной системы - определение координат, скорости, ориентации объекта-носителя, а так же обеспечение его шкалой времени. Для решения задачи оценки координат навигационного приемника, а так же коррекции его шкалы времени относительно системной, используется псевдодальномерный метод позиционирования.
Дальномерный метод позиционирования
Псевдодальномерный метод позиционирования спутниковых радионавигационных систем второго поколения является усложнением дальномерного метода позиционирования. Дальномерный метод позиционирования - это метод определения положения по измерениям дальности (расстояния) до нескольких точек с известными координатами.
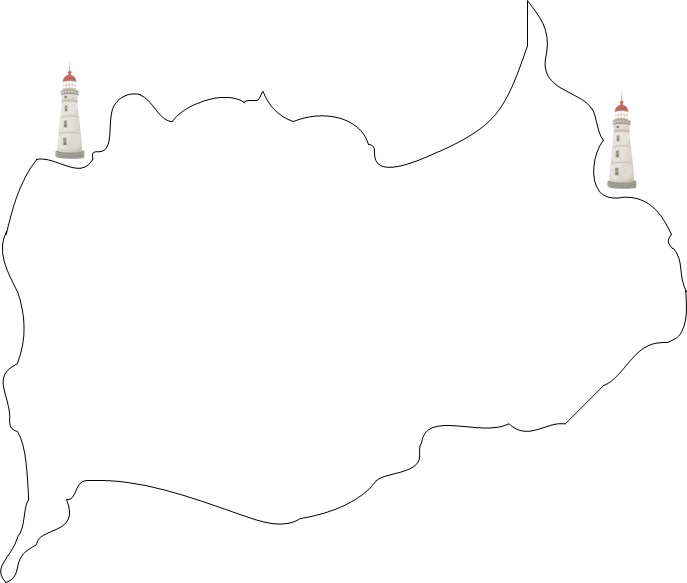
Рисунок 1 - Карта, с нанесенной береговой линией и расположением маяков
Поясним суть дальномерного метода на примере. Представим, что потребитель - это корабль в море, которому для продолжения плавания требуется узнать где же он расположен. На корабле есть часы, по которым матросы узнают время. На берегу изобретательные люди установили два маяка, как показано на рисунке 1).
Капитан предварительно договорился со смотрителем первого маяка, что ровно в полночь, и не наносекундой позже, тот подаст сигнал. Около полуночи матросы собрались вокруг корабельных часов, и как только получили сигнал - записали показания часов. На часах, естественно, было немного за полночь. Скажем, на 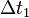 . Если известна скорость распространения сигнала
. Если известна скорость распространения сигнала 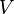 , то сразу можно сказать, что расстояние между первым маяком и кораблем составляет
, то сразу можно сказать, что расстояние между первым маяком и кораблем составляет 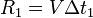 . Тогда штурман может взять карту, циркуль и начертить окружность радиусом
. Тогда штурман может взять карту, циркуль и начертить окружность радиусом  вокруг первого маяка.
вокруг первого маяка.
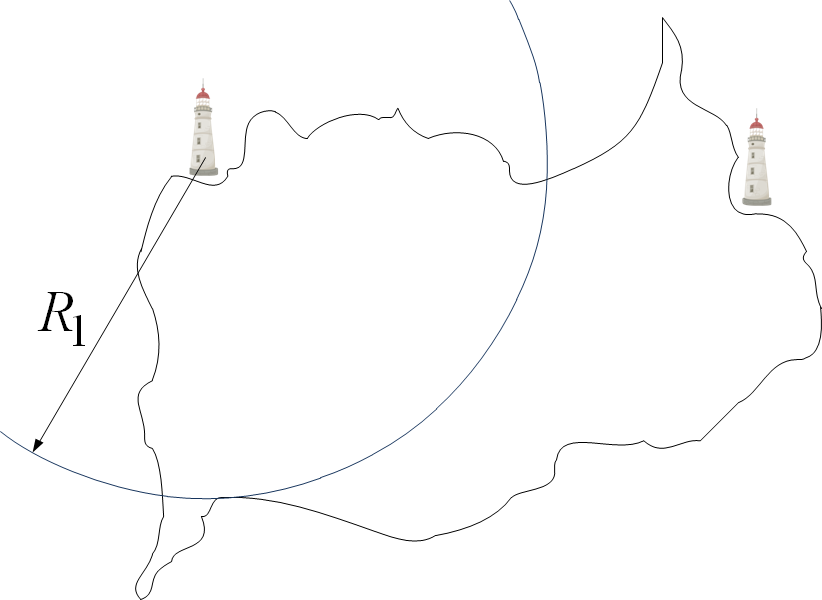
Рисунок 2 - Линия возможных положений после первого измерения
Уравнение этой окружности можно записать как:
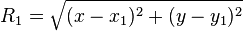 ,(1)
,(1)
где 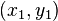 - координаты первого маяка.
- координаты первого маяка.
В любой из точек окружности, что попали в море, может находиться корабль. Это уже лучше, чем полная неопределенность, но хотелось бы ограничиться одной возможной точкой. Для этого необходимо повторить измерения расстояния до второго маяка - получить оценку 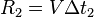 . Множество возможных положений, при которых расстояние до второго маяка составляет
. Множество возможных положений, при которых расстояние до второго маяка составляет 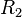 - ещё одна окружность. Её уравнение дополняет первое:
- ещё одна окружность. Её уравнение дополняет первое:
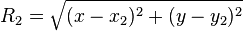 , (2)
, (2)
где 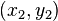 - координаты второго маяка.
- координаты второго маяка.
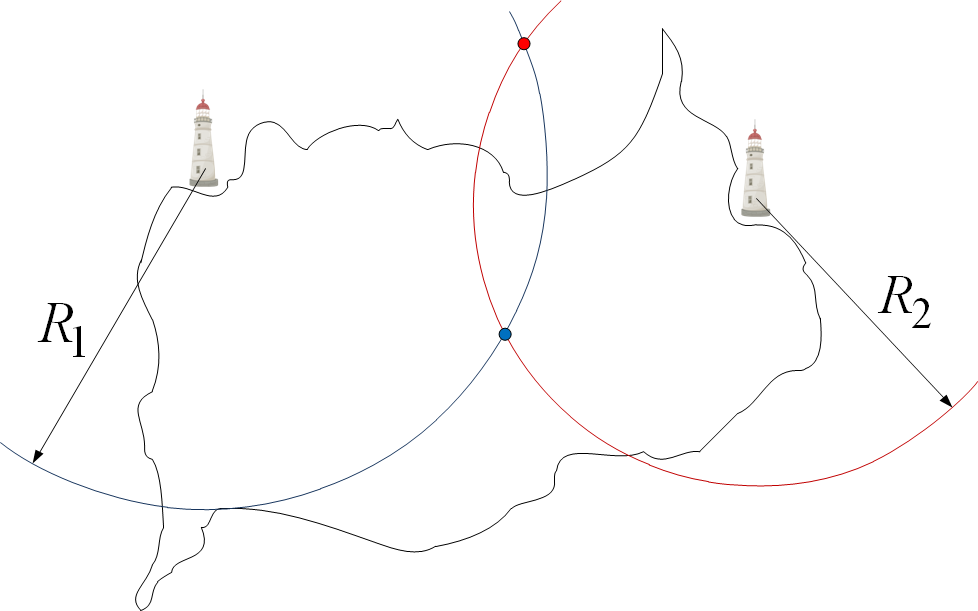
Рисунок 3 - Линия возможных положений после проведения двух измерения
Наш корабль должен одновременно находиться и на одной, и на другой окружности. Таких точек, а это точки пересечения окружностей, всего две. Но одна из них находится на суше, а морякам достаточно выглянуть за борт, чтобы понять, что они всё же в море. Остается один претендент - точка в море, которая и есть измеренное положение корабля.
Задача
Предположим, что в качестве сигнала использовалась вспышка света, а расстояние до первого маяка составляет 1000 км. Что показали часы в первый раз?
Задача
Допустим, часы на корабле запаздывают на 1 мс. Оцените вызванную этим фактом погрешность определения координат.