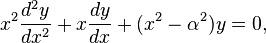Функции Бесселя — различия между версиями

Версия 22:47, 16 апреля 2011

Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

$x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,$

где $\alpha$ — произвольное вещественное число, называемое порядком.

Модифицированные функции Бесселя

Модифици́рованные фу́нкции Бе́сселя — это функции Бесселя от чисто мнимого аргумента.

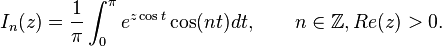
Первого рода: $I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.$

Модифицированные функции Бесселя первого рода при синтезе некогерентных систем

Исходный материал в исполнении Александра Ивановича доступен тут.

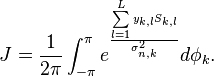
При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида: $J = \frac{1}{2\pi}\int_{-\pi}^\pi e^{\frac{\sum\limits_{l=1}^L y_{k,l}S_{k,l}}{\sigma_{n,k}^2}} d\phi_k.$

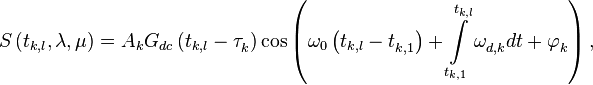
Рассмотрим подробнее числитель экспоненты для типичной модели сигнала $S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}{G}_{dc}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\varphi _{k}^{{}} \right),$

тогда

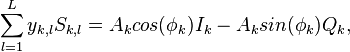
$\sum_{l=1}^L y_{k,l}S_{k,l} = A_{k}cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k},$

где

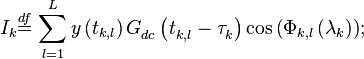
${{I}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\cos \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)};$

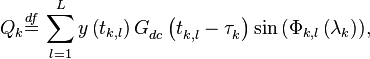
${{Q}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\sin \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)},$

в которых

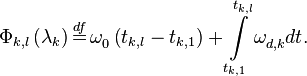
${{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,\omega _{0}^{{}}\left( {{t}_{k,l}}-{{t}_{k,1}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}.$

Далее производится красивый хак: очевидно, что 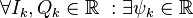$\forall I_k, Q_k \in \R {\ }: \exists \psi_k\in \R$ , такая что:

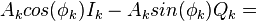
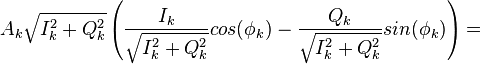
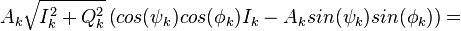
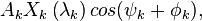
$\!\! A_{k} cos(\phi_k){I}_{k} - A_{k}sin(\phi_k){Q}_{k} = \!\!$ $A_{k} \sqrt{I_k^2 + Q_k^2} \left( \frac{I_k}{\sqrt{I_k^2 + Q_k^2}} cos(\phi_k) - \frac{Q_k}{\sqrt{I_k^2 + Q_k^2}} sin(\phi_k) \right) =$ $A_{k} \sqrt{I_k^2 + Q_k^2} \left( cos(\psi_k) cos(\phi_k){I}_{k} - A_{k}sin(\psi_k)sin(\phi_k) \right)=$ $A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k),$

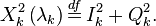
где $X_{k}^{2}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,I_{k}^{2}+Q_{k}^{2}.$

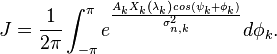
С учетом проделанных преобразованием, можно записать: $J = \frac{1}{2\pi}\int_{-\pi}^\pi e^{\frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right) cos(\psi_k + \phi_k)}{\sigma_{n,k}^2}} d\phi_k.$

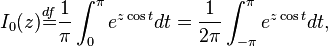
По определению, модифицированная функция Бесселя первого рода нулевого порядка: $I_0(z)\overset{df}{\mathop{=}}\frac{1}{\pi}\int_0^\pi e^{z\cos t}dt = \frac{1}{2\pi}\int_{-\pi}^\pi e^{z\cos t}dt,$

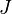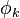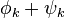тогда с учетом того, что подынтегральная функция в полученном выражении для $\!\! J$ периодична и её период совпадает с периодом интегрирования, а значит замена аргумента $\!\! \phi_k$ на $\!\! \phi_k + \psi_k$ не меняет значения интеграла, получаем выражение: $J = I_0 \left( \frac{A_{k} X_{k}\left( {{\mathbf{\lambda }}_{k}} \right)}{\sigma_{n,k}^2} \right).$

@@ Строка 15: / Строка 15: @@
 === Модифицированные функции Бесселя первого рода при синтезе некогерентных систем ===
+Исходный материал в исполнении Александра Ивановича доступен [[Media:20110416_Функция_Бесселя.doc|тут]].
 При статистическом синтезе радиосистем в случаях, когда начальную фазу сигнала относят к неинформативным параметрам, возникает задача преобразования интеграла вида:

Функции Бесселя — различия между версиями

Версия 22:47, 16 апреля 2011

Модифицированные функции Бесселя

Модифицированные функции Бесселя первого рода при синтезе некогерентных систем

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

SRNS Wiki

Рабочие журналы

Приватный файлсервер

QNAP Сервер

Инструменты